V tomto a následujícím díle už se podíváme na lokalizace v budově, které jsou založené na bezdrátových sítích. Začneme multilaterací, kterou pro své účely používá například armáda. Jak funguje a jak ji můžeme použít v praxi? A na co si dát pozor?
Lokalizace s přesností na místnost snadno a rychle (3/4)

Minule jsme si představili Dead Reckoning. Ten je založený na ukládání odchylek od daného výchozího bodu a ke svému chodu nepotřebuje žádnou síť. V tomto a posledním díle se už podíváme na to, co jsem sliboval: na způsoby lokalizace založené na příjmu signálů z různých bezdrátových sítí.
Tři dámy a jeden Kopáč
Radary určitě znáte. Jsou na každém větším letišti a jejich úkol je prostý – detekovat letící objekty. Aby to radar dokázal, musí si “vysílat” vlny, které se od daného objektu odrazí. Toho je možné využít v případě vojenského konfliktu, protože pak jde snadno zjistit, jestli nepřítel náhodou nepoužívá radar.
Problém s odhalením radaru se snaží řešit pasivní systémy. Ty nevysílají vlny, ale pouze poslouchají v určitém frekvenčním pásmu. Když nad tímto lokátorem letí letadlo, tak jeho vysílání, třeba komunikace, je odposlechnuto. Díky dalším lokátorům v okolí pak lze odvodit, kde se letadlo na obloze nachází. Pozor, u této metody nejde vůbec o obsah toho, co se vzduchem posílá. Obsah vysílané komunikace není vůbec podstatný.
U nás se pasivní radiolokátory začaly vyvíjet už v 60. letech, první byl Kopáč. Postupem času vznikla Ramona, Tamara a aktuálně je nejnovější Věra. Na této metodě je pozoruhodné, že dokáže odhalit i letadlo, které je pro radary neviditelné (Stealth letouny). Pro jeho odhalení stačí, aby komunikovalo s okolím.
Udělejme to naruby
Radiolokátory jsou de-facto velké uši, které poslouchají a čekají, aby mohly zaznamenat nějaké vysílání generované letadlem. Jinak řečeno, je to několik přijímačů a pouze jeden vysílač. Kdybychom tento koncept jen slepě okopírovali do prostředí přístupových bodů a telefonů, tak akorát zjistíme, kde je přístupový bod. My ale chceme zjistit, kde je uživatel s telefonem.
Jsme totiž v opačné situaci – potřebujeme zjistit polohu přijímače za asistence několika přístupových bodů. Ale kolika? Abychom určili jejich počet, musíme nejdříve pochopit, jak se šíří signál od přístupového bodu.
Kružnice a koule
Teď přichází má oblíbená část, ta matematická. Nebojte se, nic složitého to nebude. Signál vysílaný přístupovým bodem se v otevřeném prostoru šíří do všech směrů. Můžeme tedy okolo přístupového bodu udělat pomyslnou kouli, která představuje dosah tohoto zařízení.
Aby veškeré výpočty byly ještě jednodušší, ukážu je ve dvourozměrném kartézském prostoru. Ten nám najednou udělá z koule kružnici. To nám nicméně nevadí, protože z analytické geometrie známe rovnici, která definuje kružnici:
![]()
Možná je vám tento vzorec povědomý, protože se jedná o Pythagorovu větu v bleděmodrém. Kružnice je definována jako nekonečný počet bodů se stejnou vzdáleností od středu. Tento střed má souřadnice definovaná dvojicí [m,n] a bod na kružnici má souřadnice [x,y]. Když z těchto bodů vytvoříme vektor, bude mít velikost r. To je současně poloměr kružnice.
K čemu nám to je? r nemusí představovat maximální dosah přístupového bodu. Může představovat vzdálenost přijímače od přístupového bodu. Jak ji získáme? Na základě síly signálu. Můžeme si ji představit jako jednotku vzdálenosti, a tak ji taky použít. Střed kružnice následně představuje pozici přístupového bodu v prostoru.
Víme, jak reprezentovat přístupové body a víme, jak reprezentovat jejich přijímanou sílu signálu, ale co vlastně hledáme? Místo, kde jsou si rovny přijímané síly signálů. Neboli hledáme u kružnic bod, odkud je vzdálenost vůči středům rovna poloměrům – průsečík kružnic. Jak to matematicky napsat? Soustavou rovnic:
![]()
![]()
![]()
Tato soustava představuje způsob, jak za pomoci signálů přijímaných od tří různých přístupových bodů můžeme vypočítat pozici, která je schovaná ve dvojici [x,y]. Vypadá to sice, že je tu víc neznámých, ve skutečnosti to tak ale není. Za r se dosadí síly přijímaných signálů a do dvojic [m,n] zase polohy přístupových bodů. A proč jsou tam tři rovnice, když se snažím určit pozici ve dvourozměrném prostoru? Ano, stačí dvě rovnice na výpočet dvou neznámých, ale může se stát, že nebude platné pouze jedno řešení, ale dvě. A teď které je to lepší? Které je to víc správné? Tento problém elegantně obejdeme přidáním další rovnice, která blíže specifikuje správné řešení.
Matematickými rovnicemi přicházíme o jednu důležitou informaci – jak to vypadá nakreslené?
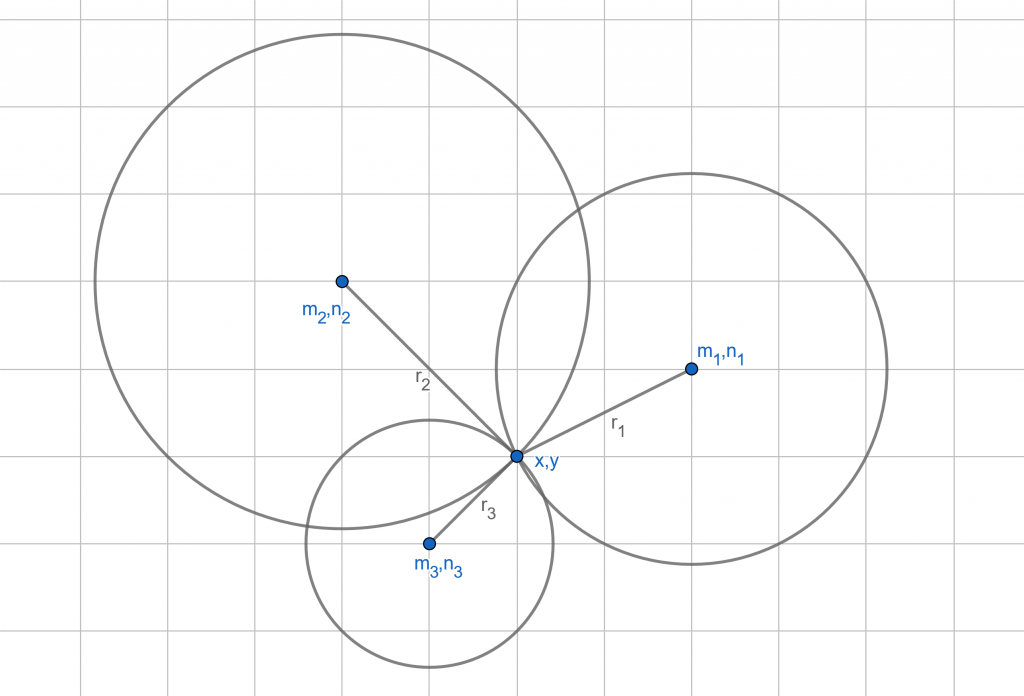
Může to vypadat například takto. Schválně jsem do nákresu dal mřížku, aby bylo na první pohled vidět, že mezi souřadnicemi středu a neznámého bodu je odvěsna reprezentující vzdálenost.
Daleko od ideálu
Na závěr můžu říct, že tato metoda je přesná. Analyticky se jedná o nejpřesnější metodu ze všech jmenovaných. Je potřeba znát přesně polohu přístupových bodů. To není zase takový problém, protože můžeme mít takovou databázi dostupnou v telefonu.
Dále je potřeba zajistit, aby na každém myslitelném místě v budově měly signál čtyři přístupové body, pokud se bavíme o vícepatrové budově. Jinak stačí tři. To také není neřešitelné, protože není potřeba mít WiFi přístupové body, ale postačí i bluetooth beacony.
Je tu ale jiný problém, v měření síly signálu. Z povahy věci telefon nikdy přesně nezměří přesnou sílu přijímaného signálu. V tom je ta schovaná podpásovka: Co když je přístupový bod za zdí? Přijímaný signál bude slabý. Telefon to vyhodnotí tak, že přístupový bod je daleko, třeba pět metrů. Ve skutečnosti je ale půl metru, jen přes zeď. To tato metoda neodhalí.
A proto je dobré trošku kopírovat od armády. Tato metoda je tedy vhodná pouze do volných prostor bez překážek. Do budovy plné stěn se nehodí. Do takové budovy se nehodí žádná metoda, která se snaží odvodit vzdálenost od vysílače podle přijímaného signálu.
Závěrem
A největší kouzlo si nechám na poslední díl seriálu. V třírozměrném prostoru je velice podobné. Jen je potřeba přidat do rovnice další rozměr a soustavu rozšířit o další rovnici.